This page is still under construction.

https://www.mcgill.ca/biochemistry/files/biochemistry/404_silvius_15.pdf

https://www.biophysics.org/Portals/0/BPSAssets/Articles/vbloomfield.pdf

Analytical Ultracentrifugation

Analytical ultracentrifugation is technique that can seperate macrmolecule that are suspended in solution in a centrifugal force field. An analytical ultracentrifuge can 'watch' molecules while they are seperating and indentify and differentiate them by their hydrodynamic properties and partial concentration. AUC works by applying a centrifugal force, causing molecules to become seperated based on their bouyant mass and their frictional properties. The molecules can be observed using different optical systems that detect the different properites of the molecules. Virtually any molecule, colloid, or particle that can be dissolved in a liquid can be measured by AUC, as long as it does not sediment by gravity alone. The molecule or particle can be as small as a salt ion, or as large as an entire virus particle.


EXAMPLE: Determine Sedimentation Coefficient

Consider an initially homogenous solution. It is centrifugated at 70,000 rpm. The absorbance profile at 230 nm is measured over time, writen as [time(hr), A\(_{plataeu}\)]:

[0,2.04], [1,1.84], [2,1.66], [3,1.50], [5,1.22], [8,0.90], [12,0.60].

What is the sedimenation coefficient of the particle?

SOLUTION: Lorem Ipsum



EXAMPLE: Determining a Protein's Molecular Weight

Consider a protein that is ran in a rotor at a speed of 12,000 rpm at 4-degrees C. It is in a dilute aqueous buffer whose density is that of water. When the absorbance profile is measured, it produces the following data:

If the proteins partial specific volume is 0.740 cm\(^{3}\)/g, what is its molecular weight?

Solution: M = 57,800 Da


When a solute is suspended in a solent, it is subject to several different forces.

First, we have the sedimenting/graviational force. This force is proportional to the mass of the particle and the acceleration is it experiencing. When considering a spinning rotor, this is the centrifugal force:

\[ F_{c} = \frac{mv_{tang}^{2}}{r} = m r \omega^{2}. \]

Here, \(r\) is the distance from the axis of rotation (cm), \(v_{tang}\) is the linear velocity perpendicular to the radial axis (m/s\(^{2}\)), and \(\omega\) is the angular velocity (radians/second).

\[\bf{Remember:~~~ 1 ~RPM = \frac{2\pi}{60} ~rad/sec.}\]

We can write it in terms of molar weight, \(M\) (g/mol), and Avogadro's number, \(N\).

\[ F_{c} = \frac{M}{N}\omega^{2}r. \]

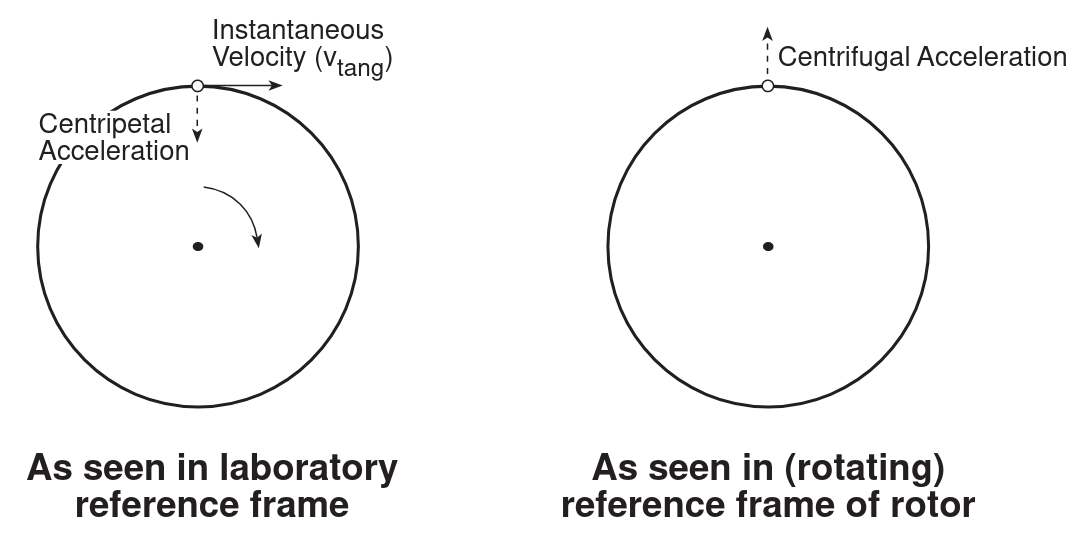
DIFFERENCE BETWEEN CENTRIFUGAL AND CENTRIPETAL: Centrifugal: in the rotating reference frame of the rotor.

Centripetal: in the labratory reference frame.

We can compare this force to the graviational force that is felt on the earth's surface. Let the radius of the earth be \(r_{e} = 6.30 \times 10^{8} cm\), the mass of the earth be \(m_{e} = 5.976 \times 10^{27}\) g. Then,

with \(G = 6.67 \times 10^{-8}\) cm\(^{3}\)/sec\(^{2}\) is the universal gravitational constant.


<span style="color: #d9534f;"EXAMPLE: Determine Centrifugal Force at Radius, r

Consider a rotor spinning at 45,000 rpm. What is its centrifugal force at a radius of 5 cm? Write as a multiple of the gravitational force.

Solution:


The second force acting on the solute is the buoyant force, \(F_{b}\):

\[ F_{b}= -m\bar\nu\rho_{0}\omega^{2}r = \frac{M}{N} \bar\nu \rho \omega^{2} r \]

where we have \(\bar\nu\) to be the partial specific volume (or the inverse of the solute's effective density), and \(\rho\) is the density of the solute. Sedimentation occurs when the density of the particle is greater than that of the solvent. As the solute moves towards the bottom of the cell, it will expereince an increase in velocity, due to the increasing radial distance (the force is proportional to radius).

As it moves through the fluid, the solute will experience a frictional drag proportional to its velocity. The frictional force is:

\[ F_{f} = -f v \]

where \(f\) is the frictional coefficent. This coefficent is dependent on the shape and size of the solute: bulky or elongated particles will experience a greater fricitonal drag compared to the drag expereinced by compact, smooth spherical particles.

The negative sign in the equations for buoyancy and frictional drag indicate that these forces are acting opposite to the sedimentation force.

As the rotor is spun up, the forces aboce will come into balance:

\[ \sum F = F_{c} + F_{b} + F_{f} = 0, \]
\[ \frac{M}{N}\omega^{2} - \frac{M}{N} \bar\nu\rho\omega^{2}r - f v = 0, \]
\[ \frac{M}{N}(1-\bar\nu\rho)\omega^{2}r - fu = 0. \]

Let us now create the term \(v/\omega^{2}r\) to represent the sedimentation coefficient, or the velocity of a particle per unit of gravitational acceleration.

\[ \frac{M(1-\bar\nu\rho)}{Nf} = \frac{v}{\omega^{2}r} \equiv s. \]

Note how this coefficient is proportional to the buoyant effective molar weight and is inversely proportional to the frictional coefficient. The sedimentation coefficent has dimensions of seconds, \(s\), and the Svedberg unit, \(S\), is defined at 10\(^{-13}\) seconds.

As sedimentation piles the solutes at the bottom of the cell, the concentration at that point will increase, and the process of diffusion will oppose further sedimentation. After an appropriate amount of time, diffusion and sedimentation will approach an equilibrium point and the concentration of the solute will have an exponential increase towards the bottom of the cell. The concentration distribution from the top of the cell to the bottom will no longer change over time and is now a function of molecular weight.

Recall that sedimentation depends on the effective molar weight, corrected for buoyancy. Consider the following cases:

\(\rightarrow\) If the density of the solute is \(\textbf{greater}\) than that of the solvent, the solute will sediment.

\(\rightarrow\) If the density of the solute is \(\textbf{less}\) than that of the solvent, the solute will float.

\(\rightarrow\) If the density of the solute is \(\textbf{equal}\) to that of the solvent, the solute will not move. Here, we can use this situation to determine the density of a macromolecule in a desnity gradient sedimentation experiemnt.

The frictional coefficient, \(f\), depends on the shape and size of the moving particle. When considering the simple case of a spherical particle, we assume the Stokes-Einstein,

\[ f = \frac{kT}{D} = \frac{RT}{ND}, \]

and the Stokes equation to hold,

\[ f = 3 \pi \eta d, \]

where \(k\) is the Boltzmann number, \(R\) is the universal gas constant, and \(d\) is the diameter of a spherical particle.

Using the formulas above, we can derive the famous Svedberg equation for determining \(M\) if \(s\), \(D\), and \(\bar\nu\) are knonw:

\[ M = \frac{sRT}{D(1-\bar\nu\rho)}. \]